
Recall, the z distribution is a normal distribution with a mean of 0 and standard deviation of 1. If we are conducting a one-tailed (i.e., right- or left-tailed) test, we look up the area of the sampling distribution that is beyond our test statistic. Because we are using the normal approximation here, we have a \(z\) test statistic that we can map onto the \(z\) distribution.
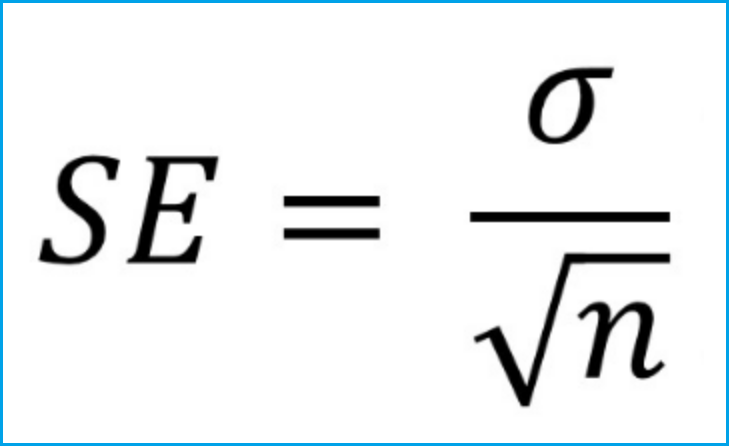
We can look up the \(p\)-value using Minitab by constructing the sampling distribution. Do not confuse this with the population proportion which shares the same symbol. Note that p-values are also symbolized by \(p\). We can find the p value by mapping the test statistic from step 2 onto the z distribution. Given that the null hypothesis is true, the p value is the probability that a randomly selected sample of n would have a sample proportion as different, or more different, than the one in our sample, in the direction of the alternative hypothesis. We will not be conducting this test by hand in this course, however you will learn how this can be conducted using Minitab using the exact method.Ĩ.1.2.1 - Normal Approximation Method Formulas 8.1.2.1 - Normal Approximation Method Formulas If \(np_0 < 10\) or \(n(1-p_0) < 10\) then the distribution of sample proportions follows a binomial distribution. Thus, this is known as a "single sample proportion z test" or "one sample proportion z test." Recall that the standard normal distribution is also known as the z distribution. If assumptions are met, the sampling distribution will have a standard error equal to \(\sqrt\) When conducting a hypothesis test, we check this assumption using the hypothesized proportion (i.e., the proportion in the null hypothesis). When constructing a confidence interval \(p\) is not known but may be approximated using \(\widehat p\). According to the Rule of Sample Proportions, if \(np\geq 10\) and \(n(1-p) \geq 10\) then the sampling distributing will be approximately normal. Indeed, S e will usually be smaller than S Y because the line a + bX summarizes the relationship and therefore comes closer to the Y values than does the simpler summary, Y ¯.

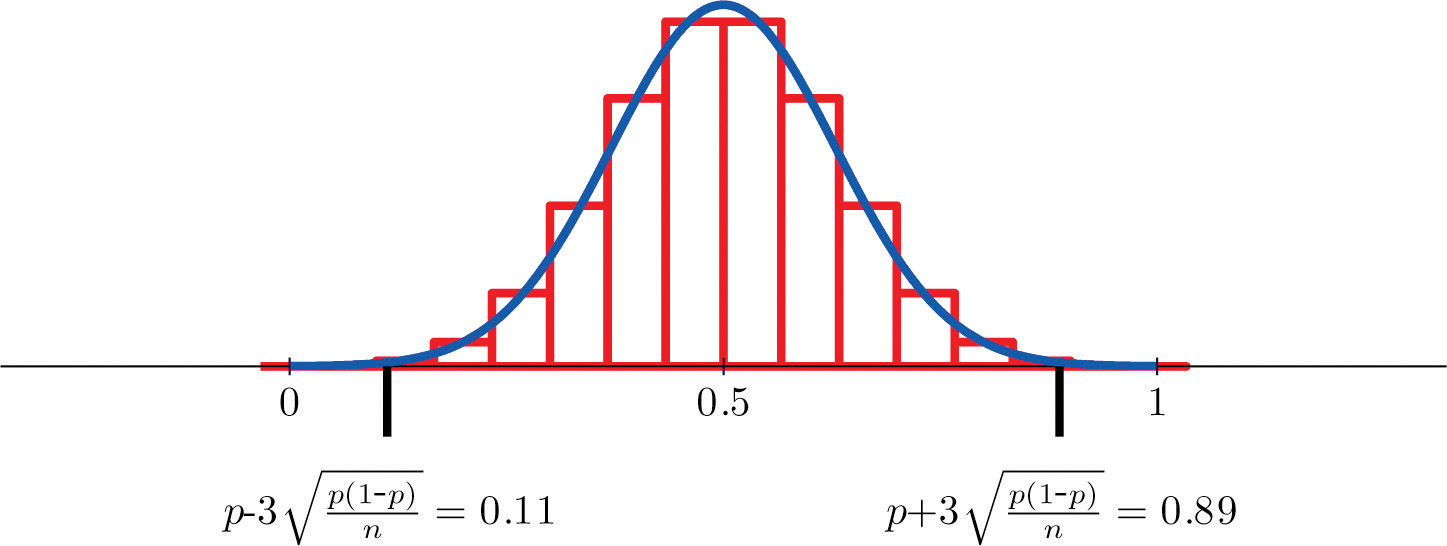
When discussion proportions, we sometimes refer to this as the Rule of Sample Proportions. For each subset T with d elements from the sample, calculate T-hat in the same way as -hat was calculated except that the elements in T are left out of the calculation. The first formula shows how S e is computed by reducing S Y according to the correlation and sample size. The Central Limit Theorem states that if the sample size is sufficiently large then the sampling distribution will be approximately normally distributed for many frequently tested statistics, such as those that we have been working with in this course. In the last lesson you were introduced to the general concept of the Central Limit Theorem. One sample proportion tests and confidence intervals are covered in Section 6.1 of the Lock 5 textbook.


 0 kommentar(er)
0 kommentar(er)
